自动机

KMP 自动机

通过预处理，实现失配时一次跳转到目标状态，而 KMP 是多次跳 $\pi$ 函数（均摊 $O(1)$）。转移方程：

$$fail[i,c]=\{\begin{array}{ll}i+1,& s_i=c\\ fail[nex{t}_i,c],& s_i\ne c\end{array}$$

WARNING

注意，这里 $nex{t}_i$ 指的是回落的位置。如果设 pi 数组表示最长非平凡公共前后缀长度，则还需要减去 $1$ 才是位置。也就是说，正确的代码是：

vector fail(n, vector<​int>(U));
for (int i = 0; i < n; ++i) {
	for (int j = 0; j < U; ++j) {
		if (s[i] == j) {
			fail[i][j] = i + 1;
		} else {
			fail[i][j] = fail[i == 0 ? 0 : pi[i - 1]][j];
		}
	}
}

AC 自动机

AC 自动机的思路和 KMP 类似，也是在失配时尽量利用已经匹配的部分来减少回退。具体来说，它把所有的模式串放在了一棵 Trie 里，然后在每次失配时跳到 Trie 中当前模式串的最长后缀的位置继续匹配。比如说，我们有模式串 $aabcd$ 和 $bce$，然后希望在字符串 $aabce$ 中找到它们。先匹配前四个字符，是 $aabc$，跟第一个模式串相等，很好，但是接下来是 $e$ 不是 $d$，于是我们需要跳到 Trie 中 $aabc$ 的最长后缀的位置，也就是 $bc$，因为 $bc$ 在 Trie 中，而更长的后缀 $abc$ 不在了。我们先来看 Trie 的构建，这一步比较简单。

vector<vector<int>> trie(1, vector<int>(26));
vector<int> tag(1);
for (int i = 0; i < n; ++i) {
    auto&& s = ss[i];
    int curr = 0;
    for (auto&& c : s) {
        int x = c - 'a';
        if (!trie[curr][x])
            trie[curr][x] = ++last,
            tag.push_back({}),
            trie.push_back(vector<int>(26));
        curr = trie[curr][x];
    }
    tag[curr] = 1;  // 标记一下模式串结束的位置
}

正如我们在 KMP 中需要处理一个 $\pi$ 函数来直接得到下一步的跳转位置一样，这里我们用 $fail$ 指针来表示 Trie 中如果在当前结点之后失配了，应该接下来跳到哪个结点。这个 $fail$ 如何计算？这里听的是董晓老师的讲解，假设我们在构建 $fail$ 数组的过程中遍历到 Trie 中的一个结点 $abc$。如果有名为字符 $x$ 的子结点，那么我们帮它建立：

$$fail[abcx]:=trie[fail[abc]][x].$$

这是一个递推的思路。假如我们已经算好了 $abc$ 的 $fail$ 指针，那么 $abcx$ 在 Trie 中的最长后缀一定是 $abc$ 在 Trie 中的最长后缀再加上一个 $x$ 字符。那么如果没有子结点是字符 $x$ 呢？那么是时候使用我们之前算好的 $abc$ 的 $fail$指针了：我们令

$$trie[abc][x]=trie[fail[abc]][x],$$

也就是它帮我们确定了走到 $abc$ 了，下个字符是 $x$ 的话失配时该怎么走。那么如何保证计算 $fail[abcx]$ 之前已经计算好 $fail[abc]$ 了呢？可以用 BFS 来确保遍历到更长的前缀串（也就是 Trie 中深度更大的结点）之前已经遍历里所有长度更短的前缀串。这一步的代码如下：

vector<int> fail(last + 1);
deque<int> dq;
for (int i = 0; i < 26; ++i) {
    if (trie[0][i]) dq.push_back(trie[0][i]);
}
while (dq.size()) {
    int c = dq.front(); dq.pop_front();
    for (int i = 0; i < 26; ++i) {
        if (trie[c][i]) {
            fail[trie[c][i]] = trie[fail[c]][i];
            dq.push_back(trie[c][i]);
        } else {
            trie[c][i] = trie[fail[c]][i];
        }
    }
}

完成这步之后，我们的 AC 自动机基本上就写好了。需要匹配的时候只需要不停沿着 $trie[curr]$ 走就可以了。我们来看模板题（洛谷 P5357）。

题目描述 给你一个文本串 $S$ 和 $n$ 个模式串 $T_{1\sim n}$，请你分别求出每个模式串 $T_i$ 在 $S$ 中出现的次数。

这题还需要统计次数，这个有点麻烦。暴力的思路是每次匹配成功的时候都把当前模式串以及所有与当前模式串后缀相同的模式串的计数都加 1，但是这复杂度比较高。但是从另一方面来说，这些后缀相同的模式串一定是当前模式串之后进行若干次 $fail$ 跳转得到的，因为它们有公共的后缀呀。一共有多少个？跳多少次 $fail$ 到达 Trie 的树根就有多少个这样的模式串。

那么我们把所有 $fail$ 边的导出子图（也就是一棵新的树，假设叫做 $fail$ 树）抽象出来，我们每次匹配时进行的操作就是在 $fail$ 树上染色，染当前结点到树根的路径上的所有结点。这个问题较为容易，可以用 DFS 解决。

vector<int> res(n);
auto dfs = [&] (auto dfs, int cur) -> int {
    int cnt = oc[cur];
    for (auto&& c : suc[cur]) {
        cnt += dfs(dfs, c);
    }
    if (cnt && tag[cur]) {
        res[id[cur]] += cnt;
    }
    return cnt;
};

这里 $id$ 数组记录了 Trie 中每个有标志的结点标志着哪个模式串的结束，而 $suc$ 是由 $fail$ 边的反向边建成的树，$oc$ 数组记录了当前结点的成功匹配次数。只需修改一点代码就可以求出 $id$ 和 $suc$。

附完整代码（C++）:

#include "../include.hh"
 
void solve(vector<string> ss, string t) {
    int n = ss.size();
    vector<vector<int>> trie(1, vector<int>(26));
    vector<int> tag(1);
    vector<int> id(1);
    vector<int> alias(n, -1);
    int last = 0;
    // build trie for ss
    for (int i = 0; i < n; ++i) {
        auto&& s = ss[i];
        int curr = 0;
        for (auto&& c : s) {
            int x = c - 'a';
            if (!trie[curr][x])
                trie[curr][x] = ++last,
                tag.push_back({}),
                id.push_back({}),
                trie.push_back(vector<int>(26));
            curr = trie[curr][x];
        }
        if (!tag[curr]) id[curr] = i;
        else alias[i] = id[curr];
        tag[curr] = 1;
    }
 
 
    // build fail
    vector<int> fail(last + 1);
    vector<vector<int>> suc(last + 1);
    deque<int> dq;
    for (int i = 0; i < 26; ++i) {
        if (trie[0][i]) dq.push_back(trie[0][i]), suc[0].push_back(trie[0][i]);
    }
    while (dq.size()) {
        int c = dq.front(); dq.pop_front();
        for (int i = 0; i < 26; ++i) {
            if (trie[c][i]) {
                fail[trie[c][i]] = trie[fail[c]][i];
                suc[trie[fail[c]][i]].push_back(trie[c][i]);
                dq.push_back(trie[c][i]);
            } else {
                trie[c][i] = trie[fail[c]][i];
            }
        }
    }
 
 
    // match t
    vector<int> oc(last + 1);
    int curr = 0;
    for (auto&& c : t) {
        int x = c - 'a';
        // if (!trie[curr][x]) curr = fail[curr];
        curr = trie[curr][x];
        oc[curr] += 1;
    }
 
 
    // collect result
    vector<int> res(n);
    auto dfs = [&] (auto dfs, int cur) -> int {
        int cnt = oc[cur];
        for (auto&& c : suc[cur]) {
            cnt += dfs(dfs, c);
        }
        if (cnt && tag[cur]) {
            res[id[cur]] += cnt;
        }
        return cnt;
    };
    dfs(dfs, 0);
    for (int i = 0; i < n; ++i) {
        if (alias[i] != -1) cout << res[alias[i]];
        else cout << res[i];
        cout << endl;
    }
}
 
int main() {
    read(int, n);
    readvec(string, ss, n);
    read(string, t);
    solve(ss, t);
}

后缀自动机

后缀自动机是一个有向无环图，每个点表示一类子串，其包括所有从源点经过转移边到达当前这个点的路径表示的子串，这些子串在原串中所有出现的结束位置构成的集合 $endpos$ 相等。有两类边：

• 转移边：从源点开始，沿着它可以走到不同的子串；
• 链接边：由某个状态转移到这个状态表示的最长子串的最长的和它 $endpos$ 不同的后缀所在的状态。

需要维护三个量：$c{h}_{vc}$ 表示 $v$ 通过字符 $c$ 转移边到达的下一个状态，$f{a}_v$ 表示 $v$ 通过链接边到达的下一个状态，$le{n}_v$ 表示 $v$ 的最长串长度。

后缀链接树

所有的链接边构成一棵后缀链接树。性质：

1. 子节点的最短串的最长后缀（也就是这个最短串删掉第一个字符）等于父节点的最长串，这是由链接边的定义直接推出的；（推论：$minle{n}_v=le{n}_{f{a}_v}+1$）
2. 一条到根的路径上，最长串的长度递减；
3. 一条到根的路径上，末尾字母是相同的；
4. 一个节点表示的子串个数是 $le{n}_v-le{n}_{f{a}_v}$；

构建

让 $p$ 从代表添加当前字符之前整个字符串所在的状态。先让 $p$ 沿着链接边不断回跳，同时让 $c{h}_{pc}$ 等于新状态，直到跳到根节点 $1$ 或者已经有 $c{h}_{pc}$ 为止。

1. 如果此时 $p=0$，说明新字符 $c$ 之前没有出现过，令 $f{a}_{np}=1$，也就是新状态 $np$ 的链接边指向根节点；
2. 如果此时 $p\ne 0$，说明 $c{h}_{pc}$ 存在，设 $q:=c{h}_{pc}$。
   1. 如果 $p$ 和 $q$ 的距离为 $1$，则令 $f{a}_{np}=q$；
   2. 否则复制一份 $q$ 到 $nq$，并令 $f{a}_{nq}=q$，$f{a}_{np}=f{a}_q=nq$。需要将 $p$ 到根的路径上所有有指向 $q$ 的点改为指向 $nq$，从 $q$ 转移的边复制给从 $nq$ 转移。

情况 2.2 的例子：

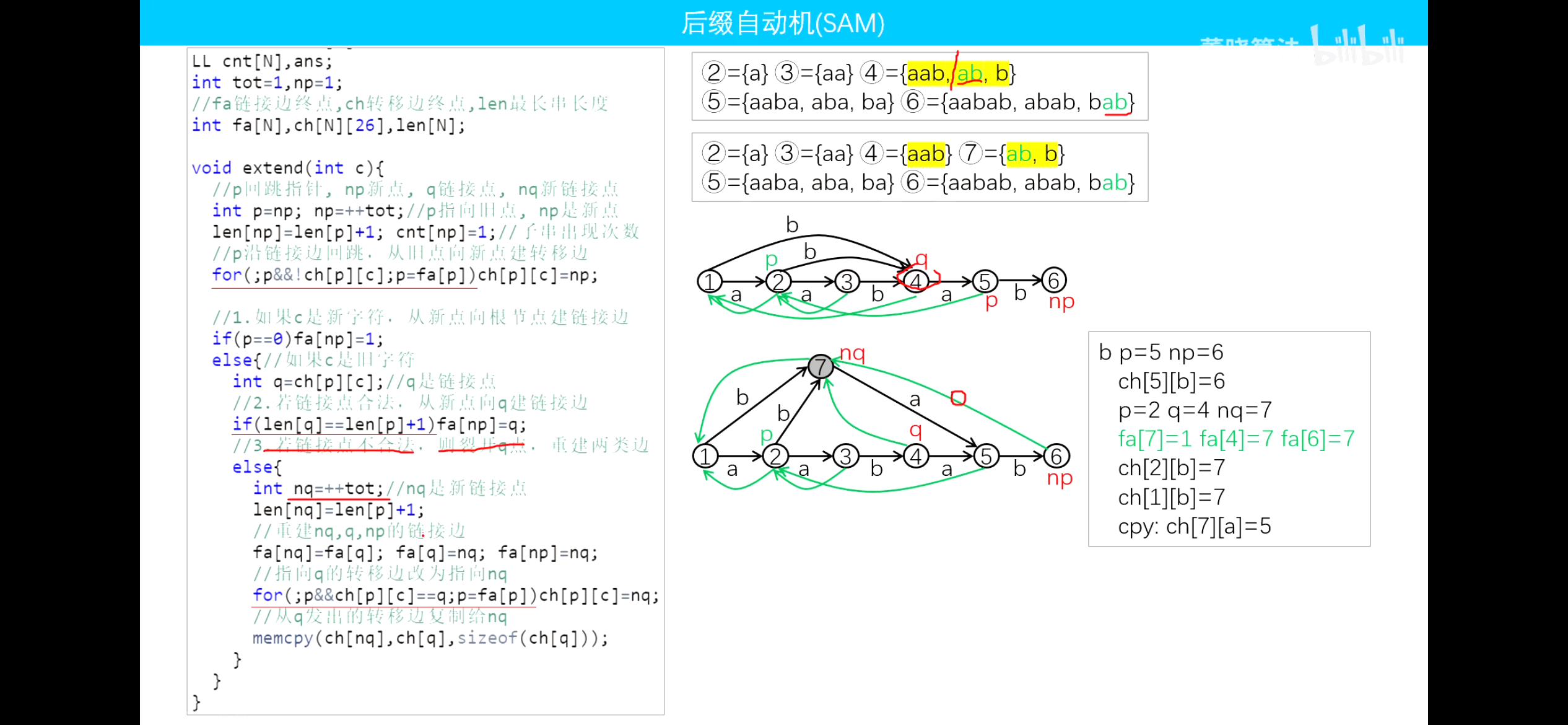
计数

要统计每个子串出现的次数，先令非复制点的 $cn{t}_v=1$，然后在树上转移 $cn{t}_{f{a}_v}+=cn{t}_v$。